Předpokládejme, že chcete zvážit dopad rizikového faktoru na dobu výskytu události. Například, Arnlov et al (2010) zvážit dopad index tělesné hmotnosti (BMI) a metabolického syndromu na rozvoji kardiovaskulárních onemocnění a smrti u mužů středního věku. Sdružení byla zkoumána pomocí údajů z kohortové studie 1758 švédských mužů středního věku s bydlištěm v jednom kraji s více než 30 lety sledování., Níže uvedený obrázek zobrazuje čas na hlavní kardiovaskulární událost podle kategorie BMI a přítomnosti (B) nebo nepřítomnosti (a) metabolického syndromu. Existuje rozdíl v těchto křivkách přežití?

Obrázek 2: Kaplan-Meierovy křivky pro hlavní kardiovaskulární příhody v různé kategorie BMI v jedinci bez MetS (a) a s MetS (B).

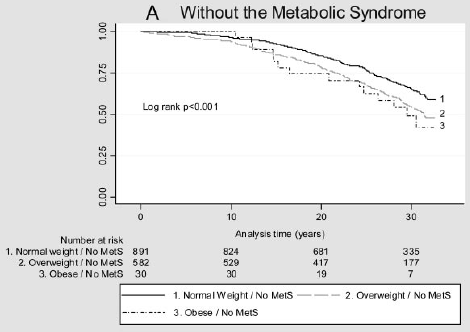
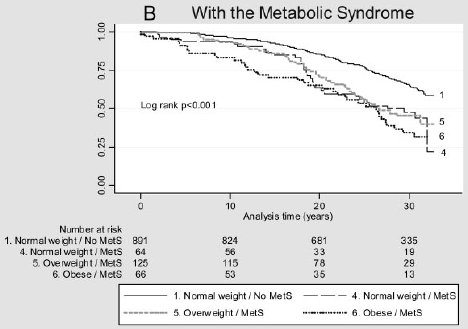
(Údaje, které jsou reprodukovány z Arnlov, J et al., Dopad indexu tělesné hmotnosti a metabolického syndromu na riziko kardiovaskulárních onemocnění a úmrtí u mužů středního věku. Circulation 2010; 121; 230-236, původně publikováno online 12/28/2009; Doi 10.1161/CIRCULATIONAHA.109.88752)

výskyt hlavní kardiovaskulární události je binární odpověď. Byla by logistická regrese s BMI jako prediktorovou proměnnou vhodná k analýze těchto dat?,

Odpověď

vztah mezi přítomnosti nebo nepřítomnosti hlavní kardiovaskulární příhody a prognostická proměnná by mohla být posuzována s logistické regrese v určitém čase, ale to by nebylo přímo porovnat křivky přežití. Analýza přežití by porovnala křivky na základě času s událostí.

metody analýzy přežití, jako je regrese proporcionálních rizik, se liší od logistické regrese hodnocením míry namísto podílu.,

regrese proporcionálních rizik také nazývaná Cox regrese, modeluje incidenci nebo míru nebezpečnosti, počet nových případů onemocnění na rizikovou populaci za jednotku času. Pokud je výsledkem smrt, jedná se o úmrtnost.
funkce nebezpečí funkce nebezpečí je pravděpodobnost, že pokud osoba přežije do t, zažije událost v příštím okamžiku.

logistická regrese naproti tomu zvažuje podíl nových případů, které se vyvíjejí v daném časovém období, tj. kumulativní incidence., Logistická regrese odhaduje poměr kurzů; proporcionální rizika regrese odhaduje poměr rizika.

poměr rizikových funkcí lze považovat za poměr rizikových funkcí, takže regresní model proporcionálních rizik lze považovat za funkci relativního rizika (zatímco logistické regresní modely jsou funkcí poměru kurzů). Změny kovariátu mají multiplikativní účinek na základní riziko. Model z hlediska funkce nebezpečí v čase t je:

\(\lambda \ left (t / X_{1i}, X_{2i},…, X_{ki} \right) = \ lambda_{0} (t)exp\left (\beta_{1}X_{1i}+\beta_{2}X_{2i}+…,+\beta_{K}X_{Ki} \right )\)

i když žádný konkrétní model pravděpodobnosti je vybrán, aby reprezentoval doby přežití, úměrné nebezpečí regrese má důležitý předpoklad: nebezpečí pro každého jednotlivce, je pevná část nebezpečnosti pro jiné jednotlivce. (tj. úměrná nebezpečí)., Všimněte si, pokud \(\lambda_0 (t)\) je nebezpečí funkce pro předmět s ukazatelem hodnoty rovny nule a \(\lambda_1 (t)\) je nebezpečí funkce pro téma s dalšími hodnoty prognostických proměnných, pak poměr rizik závisí pouze na prognostických proměnných a není na čase t. Tento předpoklad znamená, že pokud kovariance zdvojnásobuje riziko události na jeden den, to také zdvojnásobuje riziko událost na jiný den.,

Proporcionálních rizik modely mohou být použity pro diskrétní nebo kontinuální opatření čas události a může obsahovat časově závislé proměnné (proměnné, jejichž hodnoty se mohou měnit v průběhu období pozorování). Pomocí regrese proporcionálních rizik lze vytvořit poměr rizika (nebo rizika) upravený kovariátem.

vraťme se k původní otázce položené Arnlovem a colleagues…do BMI a metabolický syndrom ovlivňují vývoj kardiovaskulárních onemocnění? Přečtěte si Arnlov et al., Dopad Index Tělesné Hmotnosti a Metabolického Syndromu na Riziko Kardiovaskulárních Onemocnění a Smrti u Mužů Středního Věku Oběhu 2010;121;230-236, přičemž zvláštní pozornost je věnována statistické metody, výsledky a závěry.

Porovnejte a porovnejte poměrná rizika regresní přístup k logistickému regresnímu přístupu čtením Franco et al. Trajektorie vstupu do metabolického syndromu: studie Framinghamova srdce. Cirkulace 2009; 120; 1943-1950; původně publikováno Online 2.listopadu 2009; American Heart Association. 7272 Greenville Avenue, Dallas, TX doi: 10.,1161 / oběžník.109, 855817

můžete také porovnat výsledky obou studií. Oba dokumenty jsou ve složce čtení pro týden 14.

Poznámka! Pokud nejste obeznámeni s Kaplan-Meierovy křivky, přečtěte si Analýzu Přežití kapitola v Metody Výzkumu II monografie z Časopisu Tropických Pediatrie

(přístupné z http://www.oxfordjournals.org/our_journals/tropej/online/ma_chap12.pdf )